В прошлой статье я рассказал про 3 способа получения геокоординат из базы, входящих в радиус, и упомянул о погрешности этих методов. Однако на практике в размеченные мною круги вошли одни и те же точки, без каких-либо несоответствий. Такой пример был не нагляден, даже в какой-то степени вреден, потому что создавал видимость приемлемой точности для методов, которые сильно ошибаются. Поэтому, чтобы у читателя не возникло идеи, что разговоры о погрешности это заговор масонов или история про такие “важные” для рядового программиста вещи как проектирование спутников связи или попадание в пятирублевую монету с 20 миль, я решил показать, что происходит с точностью каждого из описанных мною способов на более крупных масштабах.
Немного о методологии. Точки, не мудрствуя лукаво, я решил использовать те же самые. А вот круги будут немного другими. Я поставлю 4 точки на удалении примерно 100 км от центра Москвы – все с разных сторон (Юг, Восток, Северо-Запад, Юго-Запад). Таким образом по центру Москвы будет проходить край большого радиуса – и на этом краю мы будем наблюдать, насколько хорошо отработала выборка. Почему окружностей всего 4 и они так расположены? Можно было поставить восемь, с каждой стороны, но тут не стоит задачи увидеть все возможные искажения. Цель – показать как в принципе себя ведут указанные методики выборки на поверхности Земли. Поэтому противоположные концы были откинуты, так как они ведут себя похоже на своих антиподов: мы можем составить представление о природе погрешности северного круга на основе южного и так далее.
Получившиеся 4 координаты такие: южная на небольшом островке на Оке, прямо под Приокско-Террасным заповедником, восточная в центра небольшого поселка Первое мая, чуть восточнее Орехово-Зуево, северо-западная где-то на берегу Малой Сестры в Клинском районе и последняя в конце улицы Дорохова в Верее. Числовое их значение можно увидеть в том же репозитории. И да, я на час залип в карту вместо написания статьи, пока эти точки выбирал…
Тестирование метода “плоской Земли”
Первый метод, основанный на представлении Земли как плоской поверхности характерен тем, что он будет ошибаться по-разному в разные стороны. Это происходит из-за того, что реальная Земля чуть-чуть сужается к северу и так же немного расширяется к югу, соответственно длина градуса, выраженная в километрах, изменяется. Так что вместо круга данный способ на карте выбирает слегка яйцеобразный эллипсоид: немного “недобирает” точек на севере и перебирает к югу. Причем по мере приближения к полюсу искажения становятся все значительнее. Для южного полушария все, естественно, наоборот 🙂
Что ж, смотрим, насколько теория соответствует практике!
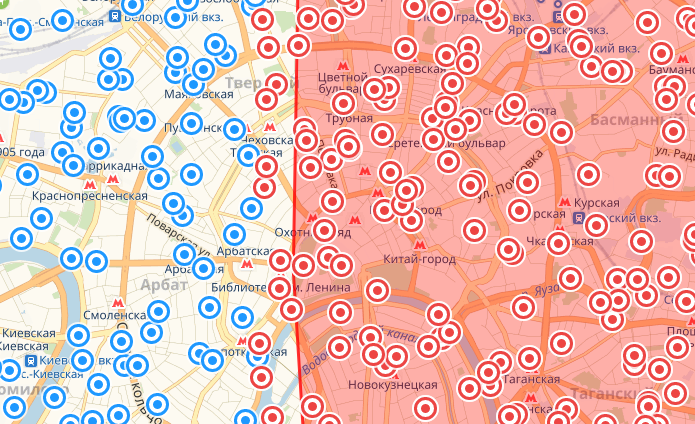
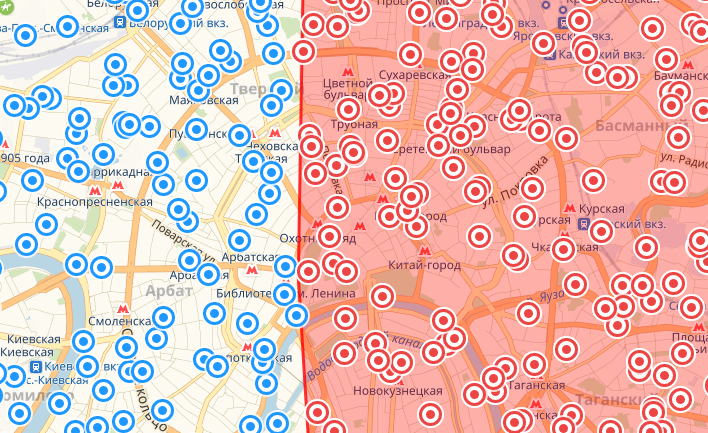
Восточная точка 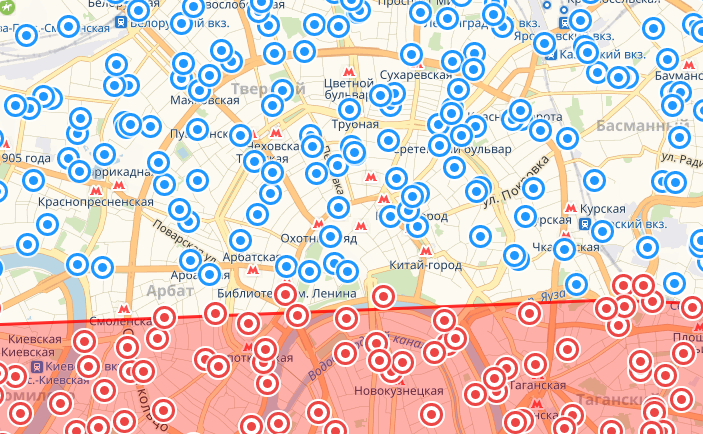
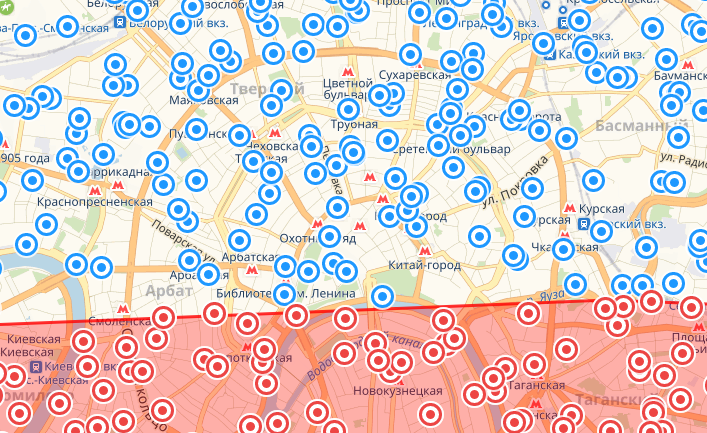
Южная точка
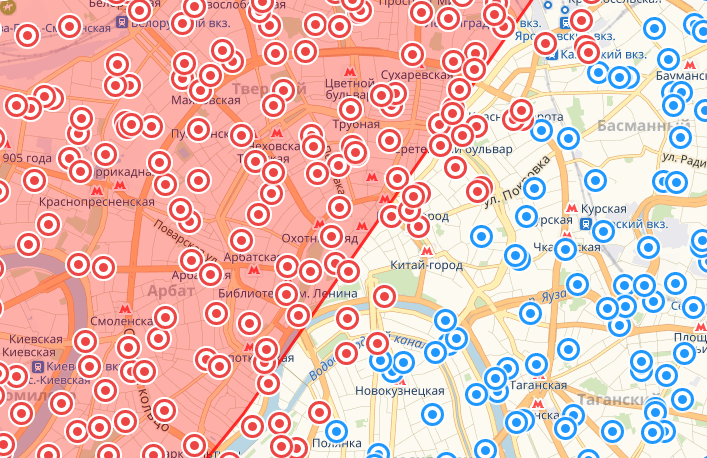
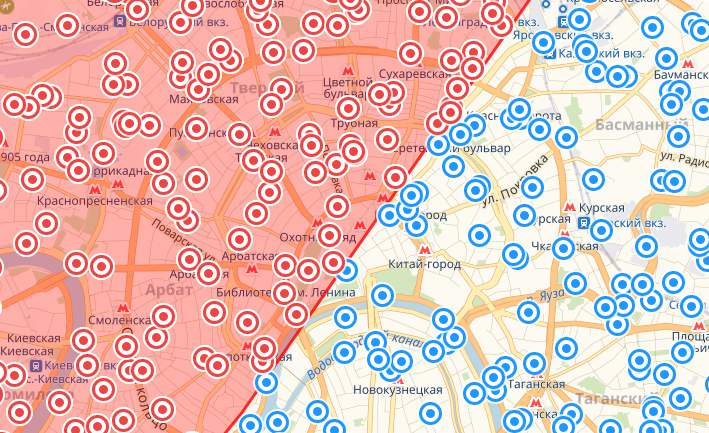
Северо-запад 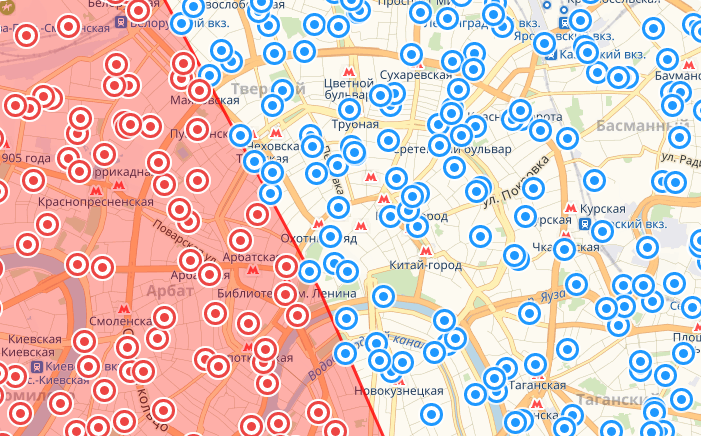
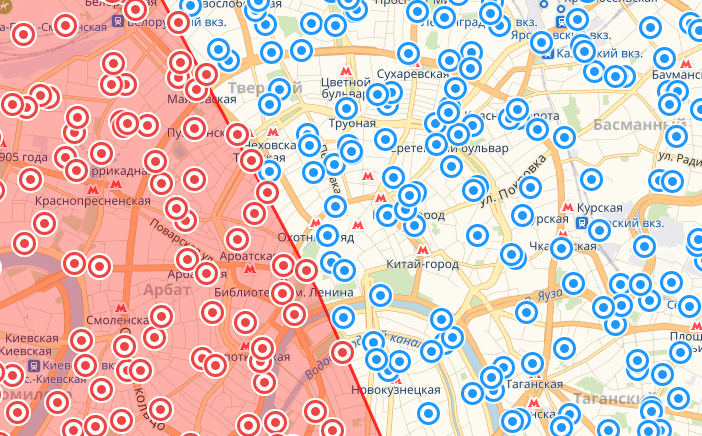
Юго-запад
Немного о том как читать картинки: точки красного цвета это те, что по расчетам попали в площадь круга. Красная фигура – реальный круг данного радиуса. Все расхождения между одним и другим – погрешность.
В целом запрос забирает чуть больше, чем необходимо со всех сторон, однако когда точки берутся с южных направлений, этот перебор нивелируется предсказанным выше недобором. При этом ошибки вдоль меридиана (на карте – по вертикали) меньше за счет того, что приплюснута Земля только с полюсов. Это уменьшает точность оценки длины градуса широты в расчетах, которые полагают Землю шаром, тогда как градус долготы практически константен. При этом максимальная наблюдаемая ошибка у меня составила 830 метров – почти 1% от радиуса круга. И самое неприятное тут то, что по мере увеличения радиуса выборки величина ошибки будет расти нелинейно.
В прошлой статье я упомянул о неточности кругов на карте Яндекса: по умолчанию построены по проекции Меркатора, но их можно сделать точнее с помощью опции geodesic. Будем ориентироваться на них. Внизу пример 2 кругов с использованием геометрической выборки точек.
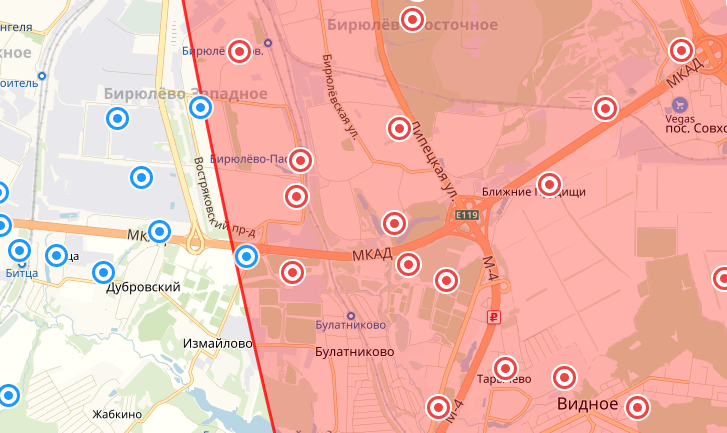
Круг по умолчанию 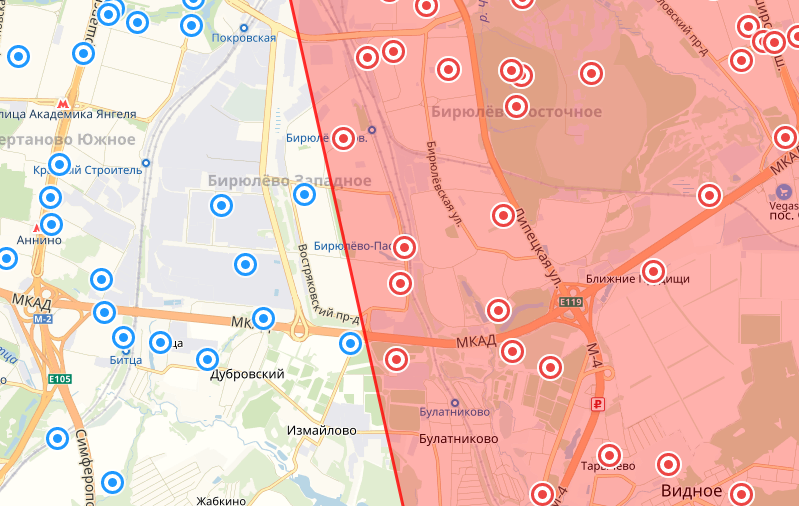
С опцией geodesic
Тестирование метода гаверсинусов
Здесь причина ошибки имеет такую же природу, как у предыдущего метода: неправильное понимание формы Земли. Однако в отличие от него ошибка не должна быть направленной, потому что моделью планеты выступает шар и происходит расчет дуги на нем. Учитывая то, что идеальный шар по площади больше, чем приплюснутый сверху аналогичного экваториального радиуса, будет разумным ожидать, что алгоритм основанный на гаверсинусах будет перебирать во все стороны. Смотрим.
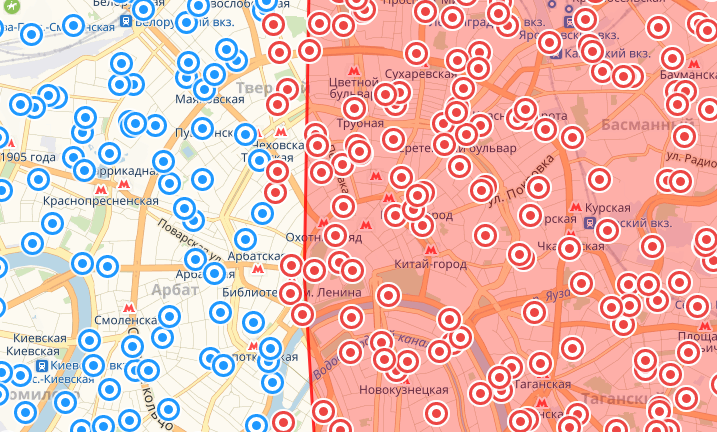
Восток 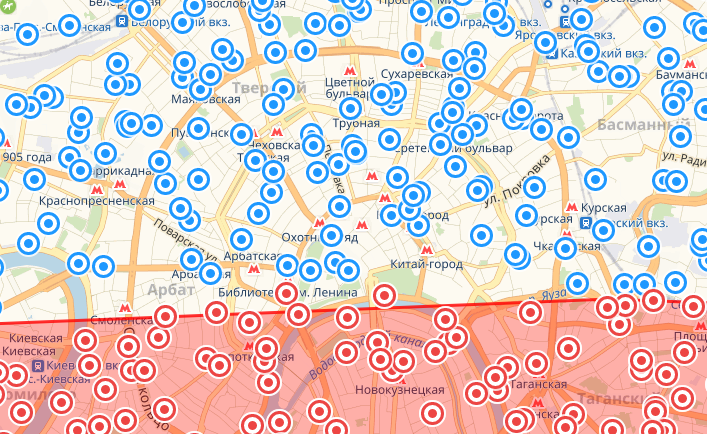
Юг
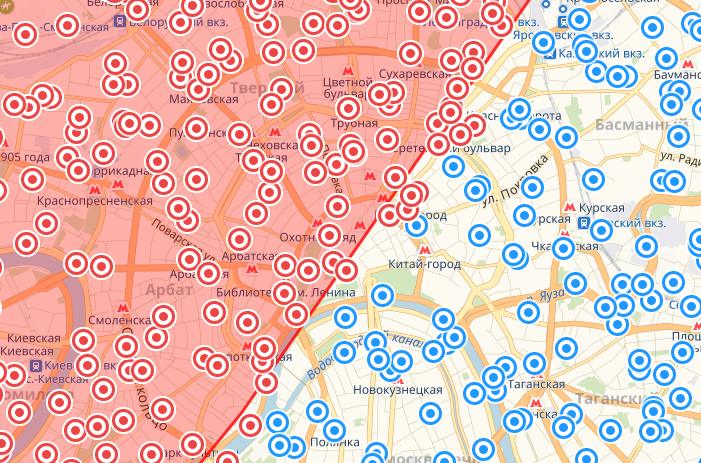
Северо-запад 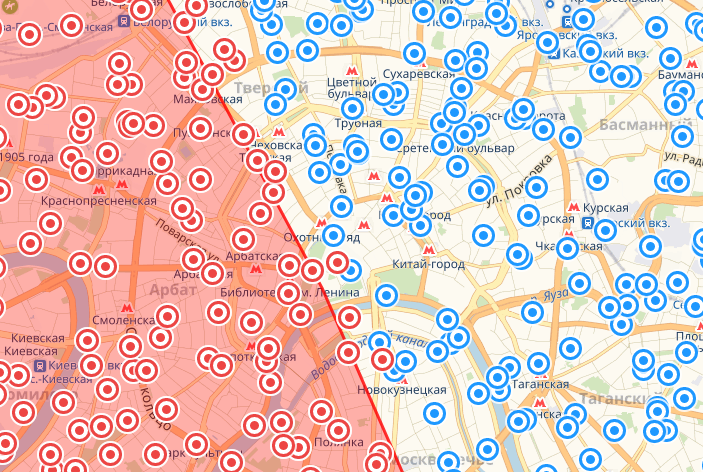
Юго-запад
В целом ошибка более-менее одинаковая и предсказуемая. Она чуть больше в некоторых случаях, однако не ошибается так безбожно, как северо-западный сценарий предыдущего способа. Ошибку в расчетах, к слову, наверняка можно понизить, подобрав более подходящее значение для константы DEGREE_LENGTH_IN_METERS = 111153. А вот плавающую ошибку на плоской карте починить нельзя никак, она там by design.
Тестирование геометрического метода
А теперь настало время фаворита. Давайте сразу смотреть результаты…
Практически идеальное совпадение. На самом деле несколько точек в каждой из выборок все-таки вывалились за круг, однако это скорее вызвано неточностью Яндекс карт: его геодезические круги не совсем круги. Скорее всего к такому решению они пришли для того, чтобы обеспечить приемлемую производительность.
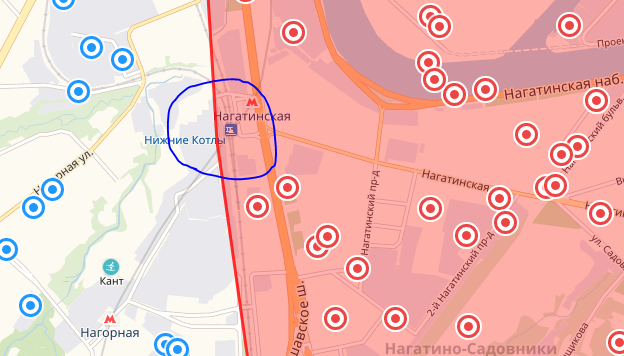
Заключение
Что ж, теперь предыдущую статью можно считать законченной 🙂 Так что выбирая метод для выборки точек можно отталкиваться не только от производительности, но и от точности методики. Однако в действительности даже 1% погрешности, который получился с плоской проекцией – это сравнительно немного. По крайней мере для прикладных задач вроде “окей, гугл, покажи мне рестораны в 5 минутах (~400 м) от меня”. Посему в общем случае мои рекомендации из предыдущей статьи останутся неизменными: лучше использовать метод гаверсинусов. Он не уступает в производительности планиметрическому, но в отличие от него, имеет предсказуемую и сравнительно небольшую ошибку в расчетах. В то же время геометрический метод требует бОльших вычислительных ресурсов, специальные колонки и индексы.