Задача по получению точек в определенном радиусе является распространенной и важной в прикладном программировании. Основная ее сложность сводится к тому, что поверхность Земли представляет собой объект сложной формы, а также в различии системы координат: точки обычно заданы в виде комбинации широты и долготы, а радиус в метрической системе. Сегодня я рассмотрю различные способы нахождения точек, попадающих в определенный радиус от заданной координаты. В качестве условия следующие вводные: БД MySQL 8, настроенная в предыдущей статье, участок земной поверхности (это будет Москва с окрестностями), а также 3000 точек, разбросанных по нашему участку. Чтобы задача была приближена к реальной, точки будут распределены не равномерно: самая большая концентрация в центре, при этом плотность падает по мере продвижения к краям карты. Работа с БД осуществляется на php 7.2 с помощью библиотеки PDO. Для визуализации данных используются Яндекс карты. Поехали.
Весь код для сегодняшней статьи можно увидеть на github, тут будут выдержки для пояснения тех или иных моментов.
Создание таблицы – тут все просто: широта, долгота и id для того, чтобы как-то отличать точки друг от друга. Сразу создам индекс, потому что я заранее знаю, по каким полям будет производиться выборка.
create table points
(
id int auto_increment,
lan double not null,
lon double not null,
constraint points_pk
primary key (id)
);
create index simple__index
on points (lat, lon);Заполнение таблицы я сделаю с помощью python библиотеки scipy.stats: я потратил полдня на то, чтобы найти пример реализации нормального распределения на php, но этот процесс мне надоел, поэтому я взял python и сделал необходимое за 15 минут. Этот язык действительно отлично подходит для подобного рода задач.
lat = norm.rvs(loc=55.75, scale=0.09, size=settings.set_size, random_state=29)
lon = norm.rvs(loc=37.62, scale=0.107, size=settings.set_size, random_state=72)Параметр scale подобран методом тыка и отвечает за размер “окна” в котором будет производиться распределение, random_state гарантирует, что от запуска к запуску результат будет одинаковым, а settings.set_size – количество точек. Последнее число определено в лежащем рядом файле settings.py – тут это 3000.
Полный код скрипта для заполнения таблицы (для удобства там же и ее создание), а также инструкция по запуску находятся в репозитории.
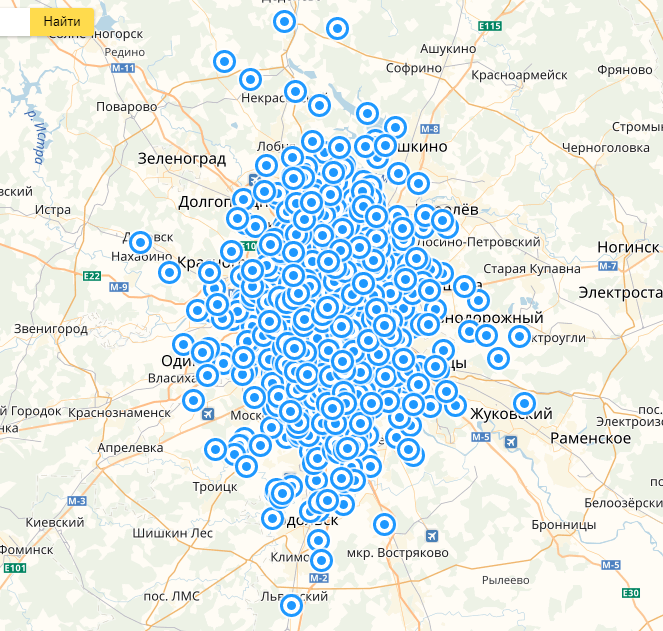
Условия выборки точек просты: 3 выборки с разным радиусом. Первая точка будет находиться ровно в Кремле и радиус выборки составит 2000 метров. Вторая – 3000 метров вокруг станции метро Сходненская и третья 4000 м. от метро Нагатинская.
Метод первый – быстрый и простой
Используем плоскую карту и теорему Пифагора.
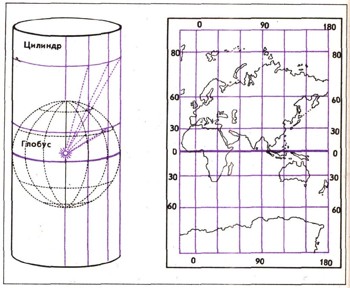
Для реализации самого простого способа решить эту задачу я применю проекцию Меркатора. В ней каждая точка на земном шаре проецируется на цилиндр, приложенный к планете, в результате чего получается хорошо знакомая прямоугольная карта. На ней более-менее точно отображаются области около экватора, а по мере приближения к полюсам точность падает, вплоть до полной невозможности как-то отобразить широты выше 85 градуса. Однако если не выполнять вычислений, затрагивающих большие площади, эта форма изображения земной поверхности может использоваться для прикладных задач. Важной особенностью проекции Меркатора является то, что направление, отмеченное на ней действительно приведет в искомую точку (не относится к варианту Web Mercator), просто прямая, связывающая точки не будет кратчайшим путем между ними. Такая линия называется локсодрома (см ссылку “почему самолёты не летают по прямой“).
Здесь, на плоской карте, можно прибегнуть к теореме Пифагора: катетами будут расстояния отмеченные по меридиану и параллели, а гипотенузой, соответственно, расстояние от точки до центра круга указанного радиуса. Дешево и сердито.
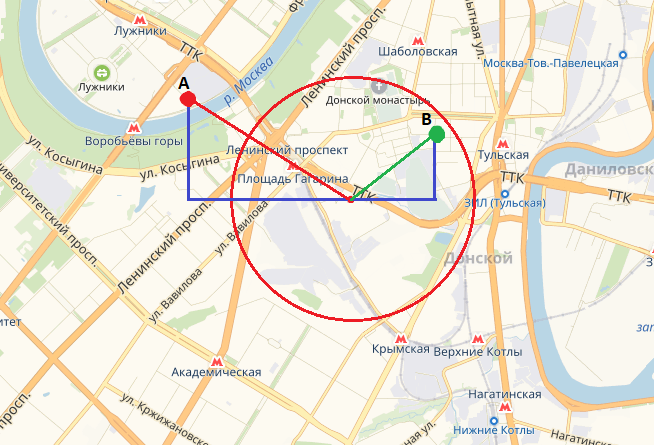
Очевидным способом оптимизировать этот запрос будет предвыборка точек с помощью простого квадрата. Нужно всего лишь найти длину в градусах по меридиану и по параллели и сделать первоначальную выборку арифметическими операторами, а расчеты радиуса применять к уже отобранным точкам. Тогда индекс, поставленный при создании таблицы упростит задачу для SQL сервера, а поиск гипотенузы будет применен только к точкам, который попали в квадрат.
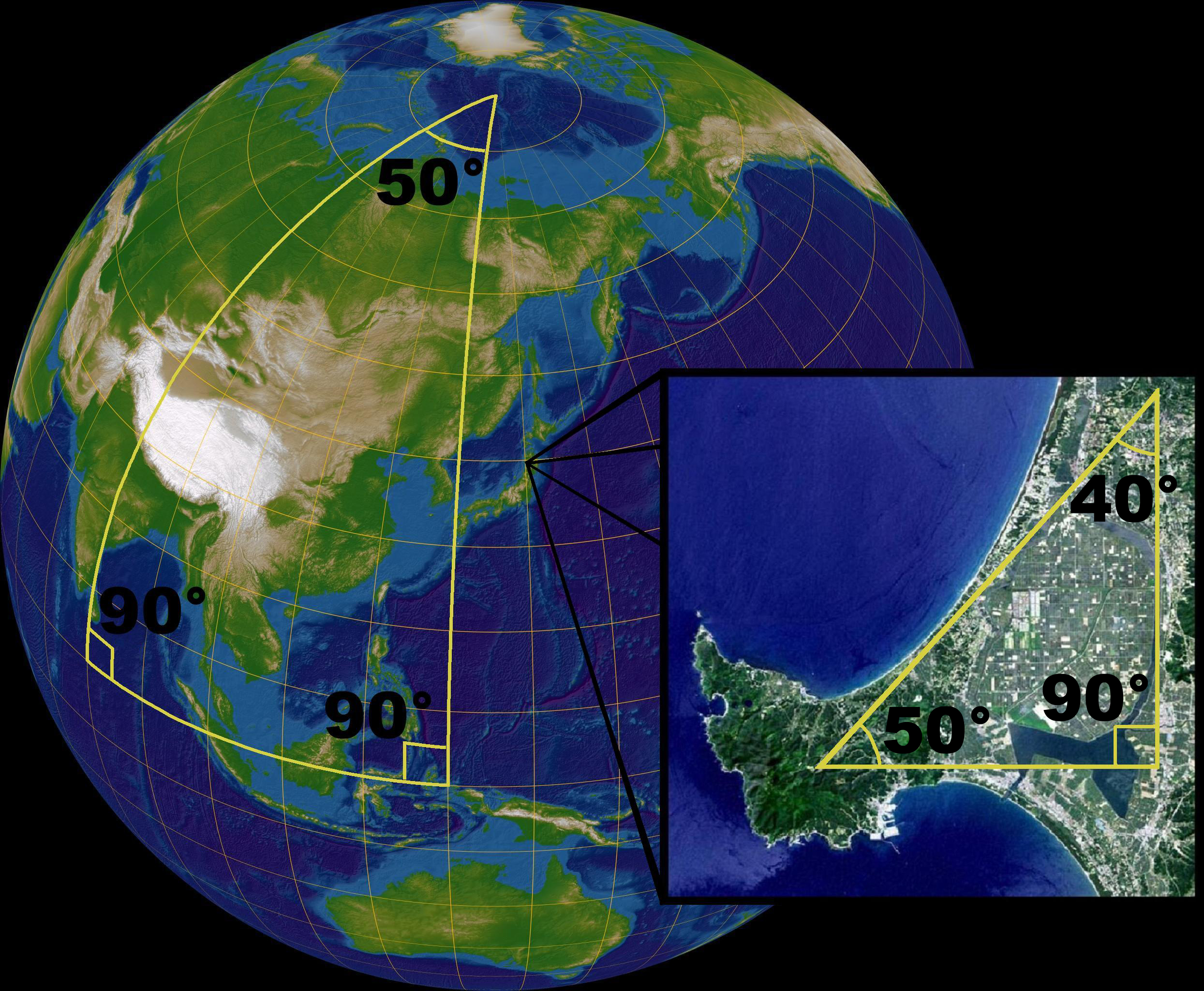
Длина одного градуса меридиана постоянна и равна примерно 111153 метрам (40015041 метров ÷ 360). С длиной градуса параллели все несколько сложнее: это число зависит от положения на земном шаре: число, получившееся выше, необходимо умножить на косинус широты. Итоговый запрос, получающий точки вокруг Кремля выглядит так (косинус и крайние точки для квадрата рассчитаны на php и подставлены в запрос):
SELECT id, lat, lon FROM points
WHERE
-- квадрат
(LAT < 55.769367216557 AND LAT > 55.733380783443) AND
(LON < 37.648729735553 AND LON > 37.584786264447) AND
-- Пифагор
POW((LAT - 55.751374) * 111153, 2) + POW((LON - 37.616758) * 62555.252801631, 2) < 4000000
ORDER BY idЭтот запрос отрабатывает очень быстро: выборка всех трех кругов произошла в среднем за 0.051 секунд при максимальном времени 0.065 и минимальном 0.041.
Замеры производились для 50 000 точек, распределенных таким же образом, как и изначальные 3000 – это количество оказалось слишком мало для того, чтобы измерения были более-менее точны. Измерялось время работы выборки всех трех групп точек. Замер времени производился с помощью php серией по 10 повторов в разное время. Так как такие замеры обладают погрешностью, наряду со средним временем я буду приводить максимальное и минимальное.
Ориентироваться на время, приведенное здесь, не стоит – оно будет сильно различаться в зависимости от железа, его загруженности и конфигурации ОС и конкретного ПО. Замеры предполагались именно как сравнение различных способов решить задачу. Однако, если читателя интересует абсолютное время, то скорее всего получится значительно быстрее, чем у меня, так как замеры производились в докер-контейнере на слабом VPS с 1.5 Гб оперативной памяти и весьма скромными данными процессора.
Скорость – это хорошо, но конечно же гораздо больше интересует то, как скрипт справился с выборкой точек. Смотрим на карту.

Общий вид 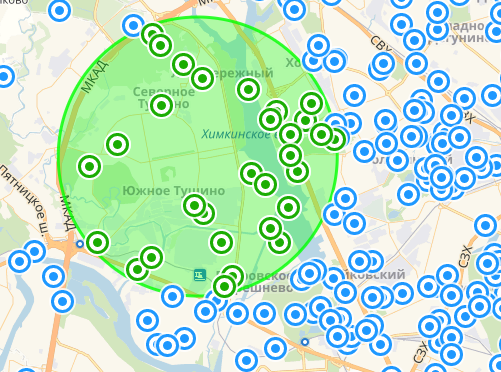
Планерная 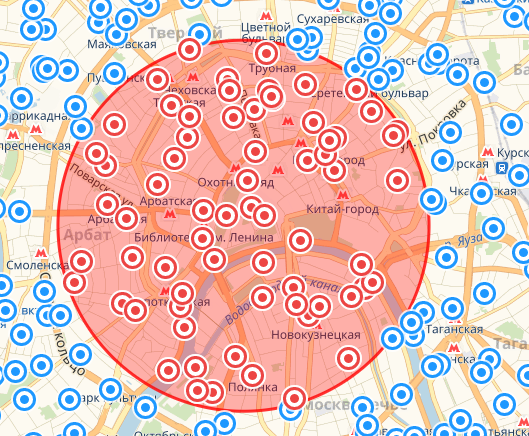
Результат запроса выше 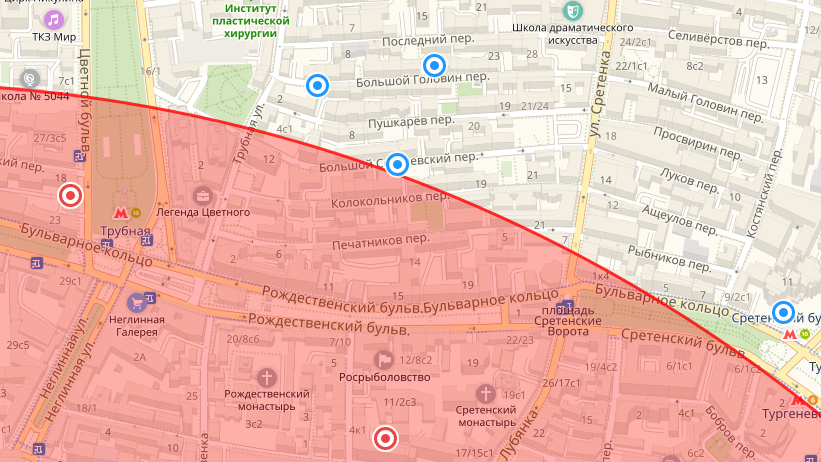
So close! На общем плане казалось, что он попадал в круг 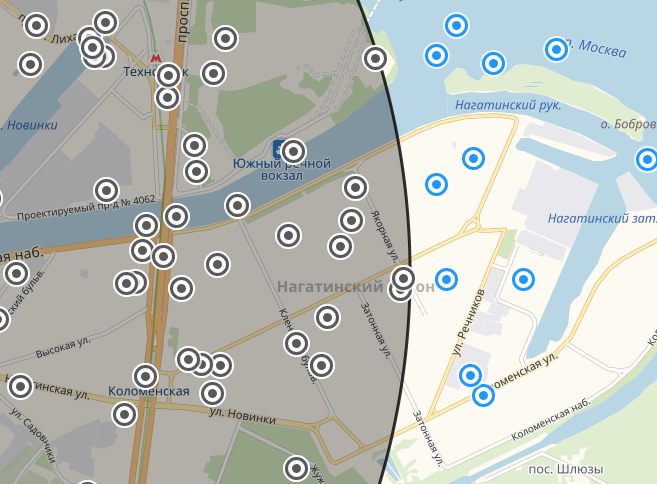
Круг у Нагатинской самый большой 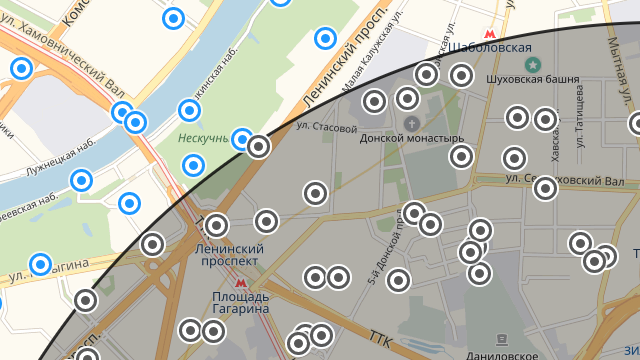
Тут тоже плотненько!
Из коробки картинки некликабельны, придется дорабатывать тему 🙂 В качестве компенсации вот ссылка, чтобы потыкать самостоятельно (осторожно, слабые компьютеры нещадно виснут на такой массе объектов!)
Здесь видно, что точки идеально попадают в круг: во всей выборке нет ни одной такой, которая была бы ошибочно приписана к радиусу или наоборот не приписана к нему. Разумеется, это не говорит об абсолютной точности методики: она просто не может быть таковой по определению. Однако для сравнительно простых случаев, вроде описанного мною, результат удовлетворяет постановке задачи.
Время исполнения запросов без “квадратной” оптимизации примерно в 3 раза больше 0.158 секунд при максимально времени 0.206 и минимальном 0.138. А EXPLAIN сообщает, что было обработано около 30% от точек, вместо всех. Так что оптимизация оправдывает себя.


В целом такой способ выборки точек в радиусе можно считать пригодным для применения. Но мы не будем останавливаться на малом. Пора рассмотреть что-то более интересное…
Метод второй – оптимальный
Используем формулу гаверсинусов для вычисления длины дуги на земном шаре.
Шар – уже несколько более хорошее приближение к форме Земли. Конечно, баллистические ракеты не полетят с такой навигацией, но прикладное программирование в принципе очень далеко от rocket science. Однако лирику в сторону, перейду к делу.
Достаточно точной для практического применения будет формула вычисления расстояния через длину дуги на шаре. Здесь применяется сравнительно редкая тригонометрическая функция синус-верзус, а точнее ее половина – гаверсинус. Подробное описание методики можно посмотреть на википедии, а здесь я просто подставлю цифры в формулу
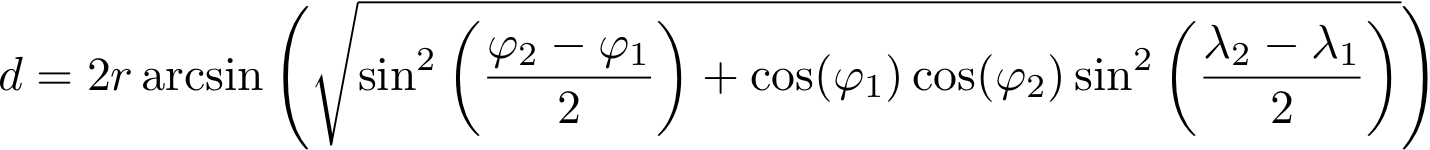
Вот та же формула на SQL. Предполагается, что переменные будут подставлены из PHP:
return <<<WHERE
6371000 * 2 * ASIN(
SQRT(
POWER(
SIN(($latColumn - ABS($lat)) * PI() / 180 / 2),
2
) +
COS({$latColumn} * PI() / 180) *
COS(ABS({$lat}) * PI() / 180) *
POWER(
SIN(({$lonColumn} - {$lon}) * PI() / 180 / 2),
2
)
)
) < {$radiusInMeters}
WHERE;Переменные $lat и $lon – координаты центра, $latColumn и $lonColumn соответственно названия колонок с широтой и долготой – их можно захардкодить. Данное условие применяется напрямую в блоке WHERE. Также можно создать функцию аналогичного содержания, куда передавать 4 координаты и возвращать результат. Я это тоже сделаю, чтобы измерить производительность каждого из вариантов.
Также я создам немного модернизированную версию этого запроса: выражение COS({$latColumn} * PI() / 180) для каждой точки является константой, и его можно хранить в отдельном столбце. Также константным значением является PI / 180 – его в оптимизированном запросе я рассчитаю на php перед вызовом и вставлю в условие. Таким образом я рассчитываю ускорить исполнение запроса.
Наконец квадрат из предыдущего примера сможет помочь и тут: все точки в круге определенного радиуса гарантированно попадают и в квадрат, так что здесь он тоже будет применен.
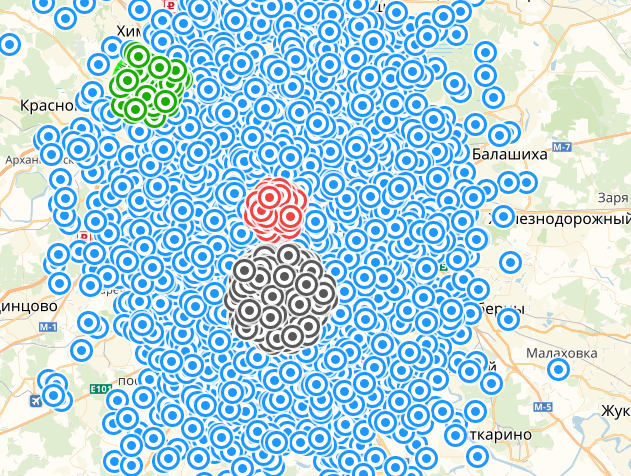
Много картинок тут не будет, потому что результаты оказались абсолютно идентичны результатам предыдущего запроса. Кстати, раз уж зашла речь о визуализации, то попадание точки в круг, нарисованный на Яндекс картах это не гарантия того, что она находится в искомом радиусе от центра. Т.к Яндекс свой картографический сервис сделал на основе меркаторовской проекции из предыдущего примера. Впрочем в данном случае масштаб по-видимому действительно слишком мал для заметных искажений.
А что с замерами? На первый взгляд кажется, что запрос значительно тяжелее, нежели предыдущий и время работы должно вырасти, однако результаты приятно удивляют. Время исполнения с среднем составило 0.056 сек. (0.068, 0.044) – что на 8% больше, чем первый вариант, однако учитывая неточность измерений это незначительная разница. Но дальше начались сюрпризы. Так среднее время работы оптимизированного запроса составило 0.089 сек. (0.145, 0.051). У меня нет точного ответа на вопрос почему, однако я предположил, что возможно дело в дополнительном столбце и накладных расходах на работу с ним. Составим еще один вариант запроса, пусть на этот раз он не будет обращаться к “лишнему” столбцу. Здесь появляется нечто похожее на результат: среднее время работы 0.053 сек, минимальное 0.038, максимальное 0.069. Этого слишком мало, чтобы можно было говорить об успехе оптимизации, но по крайней мере производительность не упала.
При работе с функцией все очень грустно. Среднее время работы 1.55 секунд, минимальное 1.2, максимальное больше 2. Обескураживающие результаты. Я проверил функцию 3 раза и не нашел там ошибки, которая могла бы приводить к замедлению. По-видимому это by design.
Тот же запрос (первая его редакция), но без использования индекса по lat и lon отработал за 0.110 сек (0.216, 0.076) – как видно, удачно выставленный индекс ускорил работу запроса вдвое. Правда и искажения в замерах на этом варианте вышли запредельными. Без квадратной предвыборки получилось 0.180 (0.198, 0.172), что лишь немногим больше, чем время работы запроса по методу подсчета на плоскости. Разница по скорости между ними оказалась весьма скромной.
Как итог выборка точек с помощью формулы гаверсинусов оказывается оптимальным способом решения данной задачи: при соразмеримой производительности этот метод точнее: погрешность будет составлять порядка 0,5%.
Самое интересное я, конечно, оставил на сладкое. Итак, встречаем настоящий метод для определения точек в радиусе:
Метод третий – честный
Погрешность предыдущего метода мала, но может быть недопустимо высокой, когда нужны точные значения. Такая досадная неточность вызвана тем, что наша планета никакой не шар. Она даже не эллипсоид с эксцентриситетом 1/298, о чем писали в школьных учебниках физики (хотя это уже похоже на правду). На самом деле форма Земли столь сложна, что для этого завели специальное понятие Геоид.
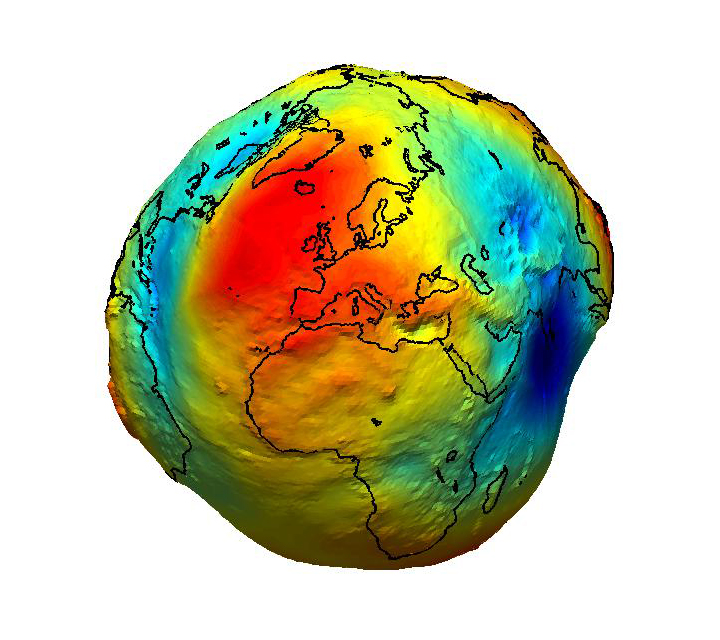
Я знаю, вы соскучились по картинкам.
Геоид наглядно (масштаб неровностей естественно не 1:1)
В общем, смоделировать нашу планету с помощью простых операторов, как я делал в предыдущих задачах, крайне нетривиальная задача. Поэтому для того, чтобы решить эту задачу “по настоящему” лучше будет воспользоваться стандартом, в котором все это уже учтено. Для работы с геометрическими запросами MySQL поддерживаются пространственные типы данных. В принципе они появились еще до 8 версии, однако в MySQL 8 стало возможным использование пространственных индексов (SPATIAL INDEX). Этот индекс позволяет хранить многомерные данные – а координаты как раз такими и являются и это должно сделать операции с ними более производительными.
Так что я добавлю в таблицу колонку с типом GEOMETRY, пространственный индекс по ней и сделаю выборку с использованием этого поля.
ALTER TABLE points ADD geom GEOMETRY NOT NULL SRID 4326;
CREATE SPATIAL INDEX g ON geometry (geom);Фрагмент “SRID 4326” сообщает SQL серверу, что будет использоваться система координат по стандарту WGS-84, основанной на центре масс Земли. Эта система используется для навигации в программном обеспечении судов, спутников, сложных информационных систем и будет гораздо точнее самодельного велосипеда на основе школьного курса тригонометрии.
Если захочется повторить все проделанное мною лично, то нет необходимости исполнять все приведенные тут запросы: в репозитории, что я указал в начале статьи, лежит скрипт, разворачивающий финальную версию таблицы с заполнением ее данными.
Составление запроса оказалось значительно проще, нежели перенос на SQL сложных формул: геометрические функции достаточно описательны и понятны. Запрос для отрисовки красного круга в этой редакции выглядит так:
SELECT id, lat, lon from points
where (ST_WITHIN(g, ST_GeomFromText(
"POLYGON( (
55.769367216557 37.584786264447,
55.769367216557 37.648729735553,
55.733380783443 37.648729735553,
55.733380783443 37.584786264447,
55.769367216557 37.584786264447 )
)",
4326
) ))
AND ST_Distance(ST_GeomFromText('POINT(55.751374 37.616758)', 4326), g) < 2000
ORDER BY idКоординаты полигона – это углы уже хорошо знакомого квадрата. Обратите внимание, что первая и последняя точка полигона равны – так мы даем понять SQL серверу, что это замкнутый полигон. Еще одна деталь, которую мне кажется важным упомянуть – каждый раз, когда используется ST_GeomFromText необходимо явно указывать систему координат, иначе она установится на дефолтную (0). В худшем случае, при разных SRID в одном запросе, произойдет ошибка.
На карте снова никаких изменений (на самом деле, для всех 3 методов выбираются одни и те же точки – я проверил это программно), а замеры показывают среднее время в 0.336 сек при максимальном 0.405 и минимальном 0.282. Долго. Заменяю полигон на квадрат из предыдущих примеров и получаю 0.156 сек (0.249, 0.128). По прежнему долго, однако уже вдвое быстрее. Возможно не работает индекс? К сожалению EXPLAIN не может сообщить ничего путного: похоже он не умеет работать с пространственными индексами, поэтому придется измерять “по живому”. Удаляю индекс.
Ой! Похоже индекс все-таки работал: без него среднее время геометрического запроса получилось 2.398 секунд (2.684, 2.216). На запрос с простым квадратом это, конечно же, не повлияло. Тут нельзя не заметить, что время исполнения с применением пространственного индекса сократилось более, чем в 7 раз – это действительно полезное нововведение.
В итоге даже с пространственным индексом самая быстрая версия по “честной” методике втрое медленнее, чем запрос основанный на формуле гаверсинусов. Честный же геометрический запрос медленнее в 6 раз. Какой-то дополнительной полезности геометрические данные не принесли, потому что отклонения на таких масштабах сравнительно небольшие и тут их вовсе не удалось пронаблюдать.
Значат ли эти результаты то, что геометрические функции не нужны и можно обойтись без них? Разумеется нет. GIS операции не ограничиваются выборкой точек в круге, есть значительное количество задач, который они могут решать. Однако конкретно для этого случая более оптимальным по сумме характеристик будет запрос, основанный на методе гаверсинусов. Так что если у вас есть таблица с геопозициями и действия с этими позициями ограничиваются получением по точному соответствию и примитивными операциями вроде выборки в радиусе и поиску ближайшей точки, можно не бежать создавать пространственные индексы и геометрические колонки.
Выводы
- Оптимальным методом для решения данной задачи является нахождение длины дуги по формуле гаверсинусов. Идеальным (и единственно верным, если точность измерений важна) метод, основанный на геометрических типах данных.
- Нет никакой причины использовать методику, основанную на плоской карте: выигрыш в производительности составляет считанные проценты, если вообще есть, а погрешность значительно выше, чем у прочих методов.
- MySQL в принципе производительная вещь: на уже описанной мною конфигурации стоковая коробка без каких-либо оптимизационных настроек собирает 3 круга из 50 000 точек за сотые доли секунды.
- Прежде чем использовать пользовательские функции в SQL нужно трижды подумать. А потом подумать еще раз. И уж точно не стоит пихать туда важную логику в запросах, где производительность важна.
- Не всякая оптимизация действительно является таковой, даже если она кажется очевидной. Любая попытка ускорить исполнение программного кода должна измеряться, иначе есть риск попасть впросак.
- Индексы нужны, иногда даже необходимы. Однако пользу от них тоже рекомендуется замерить.
- Грамотное составление запросов – половина успеха. Если где-то есть сложные расчеты, подумайте, можно ли применить какой-то грубый первоначальный фильтр для того, чтобы минимизировать число записей, участвующих в тяжелой части запроса.
Таблица со сравнением производительности запросов, экспериментальные варианты опущены.
| Пифагор | Гаверсинусы | Функция | Геометрия | Геометрия++ |
| 0.051 | 0.056 | 1.55 | 0.336 | 0.156 |
Что еще почитать по теме
Документация по пространственным типам данных в MySQL.
Статья о пространственных системах координат (SRID) в MySQL и сразу еще одна.
Метод решения подобной задачи на PostgreSQL.
Описание стандарта WGS 84.
Статья про геодезию от разработчика Яндекс Карт.
Еще про нововведения в MySQL 8 раз, два.
Проекция Web Mercator и ее особенности.
Практическая картография – хороший обзор координатных систем.
И немного развлекательного контента для тех кто дочитал:
https://thetruesize.com/ – сервис, позволяющий сравнить реальные размеры стран и материков (разрыв шаблона гарантирован).
Сравнение Земли и бильярдного шара.
Сравнение Земли и шара для боулинга.
Почему самолеты не летают по прямой – и ответы на некоторые другие вопросы о полетах.
Интерактив с точками для тех, кто пропустил ссылку в статье.